
문제 링크
https://www.acmicpc.net/problem/14725
문제
개미는(뚠뚠) 오늘도(뚠뚠) 열심히(뚠뚠) 일을 하네.
개미는 아무말도 하지 않지만 땀을 뻘뻘 흘리면서 매일 매일을 살길 위해서 열심히 일을 하네.
한 치 앞도(뚠뚠) 모르는(뚠뚠) 험한 이 세상(뚠뚠) 그렇지만(뚠뚠) 오늘도 행복한 개미들!
우리의 천재 공학자 윤수는 이 개미들이 왜 행복한지 궁금해졌다.
행복의 비결이 개미가 사는 개미굴에 있다고 생각한 윤수는 개미굴의 구조를 알아보기 위해 로봇 개미를 만들었다.
로봇 개미는 센서가 있어 개미굴의 각 층에 먹이가 있는 방을 따라 내려가다 더 이상 내려갈 수 없으면 그 자리에서 움직이지 않고 신호를 보낸다.
이 신호로 로봇 개미는 개미굴 각 층을 따라 내려오면서 알게 된 각 방에 저장된 먹이 정보를 윤수한테 알려줄 수 있다.
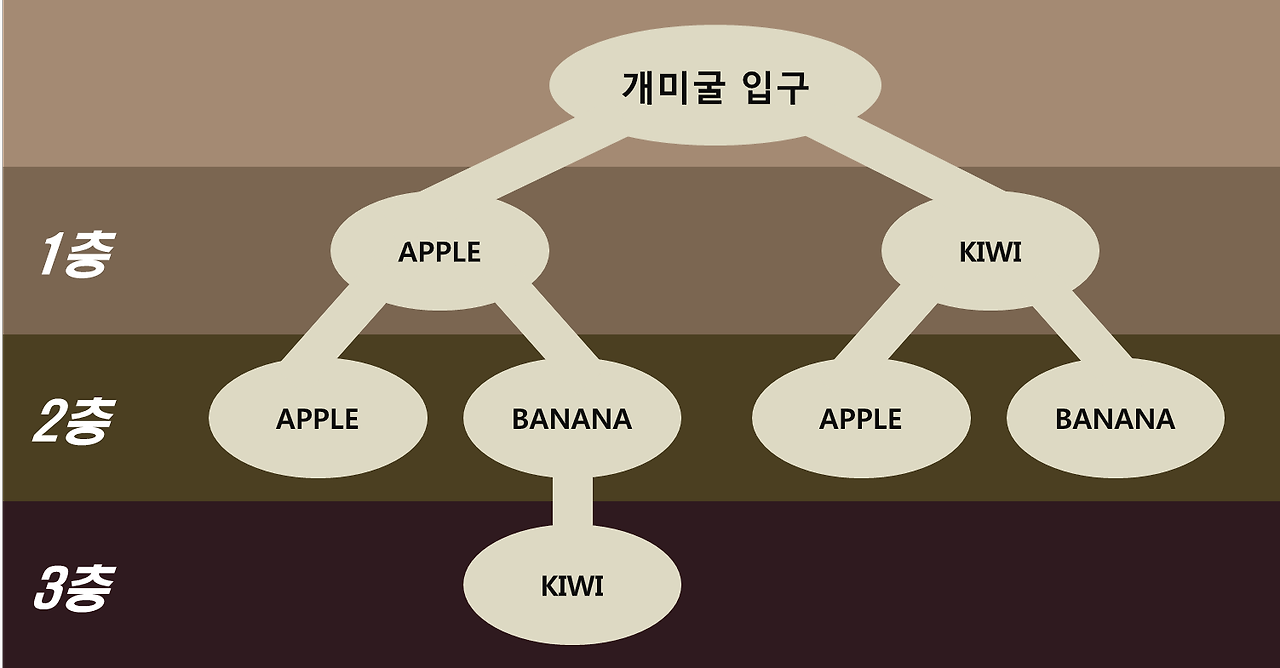
로봇 개미 개발을 완료한 윤수는 개미굴 탐사를 앞두고 로봇 개미를 테스트 해보기 위해 위 그림의 개미굴에 로봇 개미를 투입했다. 로봇 개미의 수는 각 개미굴의 저장소를 모두 확인할 수 있을 만큼 넣는다.
다음은 로봇 개미들이 윤수에게 보내준 정보다.
- KIWI BANANA
- KIWI APPLE
- APPLE APPLE
- APPLE BANANA KIWI
공백을 기준으로 왼쪽부터 순서대로 로봇 개미가 각 층마다 지나온 방에 있는 먹이 이름을 뜻한다.
윤수는 로봇 개미들이 보내준 정보를 바탕으로 다음과 같이 개미굴의 구조를 손으로 그려봤다.
APPLE
--APPLE
--BANANA
----KIWI
KIWI
--APPLE
--BANANA
개미굴의 각 층은 "--" 로 구분을 하였다. 또 같은 층에 여러 개의 방이 있을 때에는 사전 순서가 앞서는 먹이 정보가 먼저 나온다.
우리의 천재 공학자 윤수는 복잡한 개미굴들을 일일이 손으로 그리기 힘들어 우리에게 그려달라고 부탁했다.
한치 앞도 모르는 험한 이세상 그렇지만 오늘도 행복한 개미들!
행복의 비결을 알기 위해 윤수를 도와 개미굴이 어떤 구조인지 확인해보자.
입력
첫 번째 줄은 로봇 개미가 각 층을 따라 내려오면서 알게 된 먹이의 정보 개수 N (1 ≤ N ≤ 1000)개가 주어진다.
두 번째 줄부터 N+1 번째 줄까지, 각 줄의 시작은 로봇 개미 한마리가 보내준 먹이 정보 개수 K (1 ≤ K ≤ 15)가 주어진다.
다음 K개의 입력은 로봇 개미가 왼쪽부터 순서대로 각 층마다 지나온 방에 있는 먹이 정보이며 먹이 이름 길이 t는 1 ≤ t ≤ 15를 만족한다. 먹이 정보는 알파벳 대문자로만 이루어져 있다.
출력
개미굴의 시각화된 구조를 출력하여라.
개미굴의 각 층을 "--" 로 구분하며, 같은 층에 여러개의 방이 있을 때에는 사전 순서가 앞서는 먹이 정보가 먼저 나온다.
최상위 굴을 포함하여 하나의 굴에서 개미굴이 여러개로 나뉠 때 먹이 종류별로 최대 한 번만 나올 수 있다.
단순 구현으로 풀릴까?
우선 가장 쉬운 방법인 구현을 생각해보자.
층별로 먹이의 종류는 중복되지 않아야 하고 층별 동굴에선 또다른 동굴이 파생된다. 이는 트리의 모양과 동일함을 그림만 봐도 알 수 있다. 그러면 각 노드별 필요한 정보를 모아 객체를 만들면 다음과 같다.
class AntCave {
String feed; //먹이 이름
int depth; //층수
List<AntCave> next = new ArrayList<>(); //다음 동굴
}
각 층별로 현재 로봇 개미가 탐색한 먹이가 있는지 없는지 판단해서 있다면 다음 동굴로 바로 이동하고 없다면 새로운 동굴을 생성한 뒤 다음 동굴로 이동하면 주어진 상황을 구현할 수 있을 것이다. 이때 각 먹이의 이름은 알파벳 오름차순으로 정렬해야 하므로 동굴이 추가되면 알파벳 순으로 정렬해야 한다.
모든 동굴을 찾았다면 탐색을 해야한다. 층수별로 가장 위에서부터 왼쪽으로 탐색한다고 했으므로 전위탐색이다. 전위탐색을 위해 DFS로 탐색하여 현재 층수만큼 "--"을 앞에 더하여 형식에 맞게 출력하면 될 것이다.
구현의 시작복잡도를 계산해보자.
원활한 시간 복잡도 계산을 위해 수도코드로 표현하면 다음과 같다.
for(개수 1~N){
현재 동굴
for(층수 1~K){
다음 = 새로운 동굴
for(현재 먹이 : 현재 층수의 모든 먹이){
if(현재 먹이의 동굴이 있다면){
다음 동굴 = 현재 존재하는 동굴
}
}
현재 동굴 = 다음 동굴
}
}
위의 수도코드를 바탕으로 시간복잡도를 계산하면 다음과 같다.
O(N)
= (입력 개수) * (현재 층) * ((현재 층에 존재하는 모든 먹이) + (정렬)) + (모든 동굴 탐색)
= N * K * (N + logN) + K * N
≒ N^2 * logN *K
N은 최대 1,000이고 K는 최대 15이다. 그러므로 예상 연산 횟수는 1,000*1,000 * 15 * 3 = 45,000,000인데 이는 제한 시간인 1초의 연산 횟수인 1억보다 작다. 그러므로 구현으로 충분히 풀 수 있다!
해결 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main{
final static int ROOT = 0;
final static String DEPTH = "--";
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
AntCave root = new AntCave("",ROOT);
for(int n=1;n<=N;n++){
String[] input = br.readLine().split(" ");
int K = Integer.parseInt(input[0]);
AntCave curr = root;
for(int depth=1; depth <= K; depth++){
AntCave next = new AntCave(input[depth],depth);
boolean exist = false; //먹이가 현재 층에 이미 존재하는지 판단하는 변수
for(AntCave antCave : curr.next){
//이미 먹이가 있는 경우
if(next.feed.equals(antCave.feed)){
next = antCave;
exist = true;
break;
}
}
//처음 먹이인 경우 다음 동굴에 추가
if(!exist){
curr.next.add(next);
Collections.sort(curr.next);
}
curr = next;
}
}
printCave(root);
}
public static void printCave(AntCave curr){
if(curr.depth != ROOT){
StringBuilder sb = new StringBuilder();
sb.append(DEPTH.repeat(curr.depth - 1));
sb.append(curr.feed);
System.out.println(sb.toString());
}
for(AntCave next : curr.next){
printCave(next);
}
}
}
class AntCave implements Comparable<AntCave>{
String feed;
int depth;
List<AntCave> next = new ArrayList<>();
public AntCave(String feed,int depth){
this.feed = feed;
this.depth = depth;
}
@Override
public int compareTo(AntCave o) {
return this.feed.compareTo(o.feed);
}
}
실행 결과

번외 : 시간복잡도를 조금 더 줄여보자 (트라이)
class AntCave implements Comparable<AntCave>{
String feed; //먹이 이름
int depth; //층수
TreeMap<String, AntCave> next = new TreeMap<>(); //다음 개미굴 [먹이 이름 : 개미굴]
public AntCave(String feed,int depth){
this.feed = feed;
this.depth = depth;
}
@Override
public int compareTo(AntCave o) {
return this.feed.compareTo(o.feed);
}
}
이렇게 하면 다음 먹이가 있는지 containeKey를 이용해 O(1)의 시간복잡도로 찾을 수 있으면서 TreeMap을 사용하면 키 기준으로 정렬을 할 수 있으므로 코드도 더 단순화된다! 이 자료구조는 마치 끝 판정이 없는 트라이와 유사하다. 위의 방식으로 시간복잡도를 계산하면 다음과 같다.
O(N)
= (입력 개수) * (현재 층) * ((현재 층에 존재하는 모든 먹이) + (정렬)) + (모든 동굴 탐색)
= N * K * (1 + NlogN) + K * N
≒ N^2 * logN *K
N은 최대 1,000이고 K는 최대 15이다. 그러므로 예상 연산 횟수는 1,000*1,000 * 15 * 3 = 45,000,000인데 이는 제한 시간인 1초의 연산 횟수인 1억보다 작다. 그러므로 트라이로도 충분히 풀 수 있다! 시간복잡도 상으로는 차이가 없으나 내부적으로 먹이를 찾는 연산 횟수가 기존 O(N)에서 O(1)로 짧으므로 트라이가 더 효율적인 방법이라고 할 수 있다.
번외 : 해결 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
final static int ROOT = 0;
final static String DEPTH = "--";
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
AntCave root = new AntCave("",ROOT);
for(int n=1;n<=N;n++){
String[] input = br.readLine().split(" ");
int K = Integer.parseInt(input[0]);
AntCave curr = root;
for(int depth=1; depth <= K; depth++){
AntCave next = curr.next.get(input[depth]);
if(next == null){
next = new AntCave(input[depth],depth);
curr.next.put(next.feed,next);
}
curr = next;
}
}
printCave(root);
}
public static void printCave(AntCave curr){
if(curr.depth != ROOT){
StringBuilder sb = new StringBuilder();
sb.append(DEPTH.repeat(curr.depth - 1));
sb.append(curr.feed);
System.out.println(sb.toString());
}
for(AntCave next : curr.next.values()){
printCave(next);
}
}
}
class AntCave implements Comparable<AntCave>{
String feed;
int depth;
TreeMap<String, AntCave> next = new TreeMap<>();
public AntCave(String feed,int depth){
this.feed = feed;
this.depth = depth;
}
@Override
public int compareTo(AntCave o) {
return this.feed.compareTo(o.feed);
}
}'알고리즘 문제 풀이 > 해설' 카테고리의 다른 글
| [백준 - 2533][Gold 3] - 사회망 서비스(SNS) (JAVA) (0) | 2024.03.18 |
|---|---|
| [백준 - 12886][Gold 4] - 돌 그룹(JAVA) (0) | 2024.03.14 |
| [백준 - 2342][Gold 3] - Dance Dance Revolution (JAVA) (0) | 2024.03.04 |
| [백준 - 15685][Gold 3] - 드래곤 커브 (JAVA) (4) | 2024.02.29 |
| [백준 - 21758][Gold 5] - 꿀 따기 (JAVA) (1) | 2024.02.28 |

