[백준 1914][Silver 1] - 하노이 탑(JAVA)

728x90

문제 링크

https://www.acmicpc.net/problem/1914

문제

세 개의 장대가 있고 첫 번째 장대에는 반경이 서로 다른 n개의 원판이 쌓여 있다. 각 원판은 반경이 큰 순서대로 쌓여있다. 이제 수도승들이 다음 규칙에 따라 첫 번째 장대에서 세 번째 장대로 옮기려 한다.

한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.

이 작업을 수행하는데 필요한 이동 순서를 출력하는 프로그램을 작성하라. 단, 이동 횟수는 최소가 되어야 한다.

아래 그림은 원판이 5개인 경우의 예시이다.

입력

첫째 줄에 첫 번째 장대에 쌓인 원판의 개수 N (1 ≤ N ≤ 100)이 주어진다.

출력

첫째 줄에 옮긴 횟수 K를 출력한다.

N이 20 이하인 입력에 대해서는 두 번째 줄부터 수행 과정을 출력한다. 두 번째 줄부터 K개의 줄에 걸쳐 두 정수 A B를 빈칸을 사이에 두고 출력하는데, 이는 A번째 탑의 가장 위에 있는 원판을 B번째 탑의 가장 위로 옮긴다는 뜻이다. N이 20보다 큰 경우에는 과정은 출력할 필요가 없다.

문제 해석

어렸을 때 많이 했던 하노이의 탑 퍼즐을 구현하는 문제이다. 하노이의 탑은 크게 2가지의 조건이 있다.

한 번에 한 개의 원판만을 다른 탑으로 옮길 수 있다.
쌓아 놓은 원판은 항상 위의 것이 아래의 것보다 작아야 한다.

위의 조건을 지켜서 1번 위치의 있는 모든 원판을 3번 위치로 옮기는 최소 횟수와 경로를 구해야된다.

완전탐색으로 풀릴까??

경우의 수를 찾는 가장 쉬운 방법은 모든 경우의 수를 다 찾는 완전탐색이다. 만약 완전 탐색인 조합으로 모든 경우를 찾는다면 시간 복잡도는 다음과 같다.

(옮길 원판을 1, 2, 3 중 하나를 고른다) *(옮길 원판의 나머지 위치를 중 하나를 고른다.)^(원반의 개수)
= (3 * 2)^N
= 6^N

여기서 경로가 필요한 경우는 최대 20이다. 그러므로 6^20 = 3,656,158,440,062,976 이기 때문에 제한시간인 6초인 약 6억보다 매우 크다. 그러므로 다른 방법을 찾아야한다.

DP로 풀릴까??

다음으로 경우의 수를 찾는 방법인 DP를 생각해보자. DP를 사용하기 위해선 점화식, 즉 일정한 규칙을 찾아야한다. DP적인 생각하기 위해 하노이의 탑을 부분적으로 나누어서 해결해보자.

우선 기징 쉬운 나온 높이가 1인 하노이의 탑을 그려보면 다음과 같다.

바닥과 탑을 헷갈리지 않게 하기위해 바닥은 숫자로, 탑은 (1)과 같이 괄호로 표현하겠다.

1번의 탑 (1)을 오른쪽으로 옮기기 위해선 간단하게 왼쪽의 (1) 탑을 3번으로 한번 옮겨주기만 하면된다. 그러므로 1번의 탑을 3번으로 옮기기 위한 최소 이동 거리는 1이다.

다음으로 높이가 2인 하노이의 탑을 그려보면 다음과 같다.

이제 1번 위치에 있는 (1,2) 탑을 3번으로 옮기기 위해서는 우선 가장 아래에 있는 (2) 탑을 3번으로 옮겨야한다. 그러므로 (2)탑 위에 잇는 (1) 탑을 빈칸인 2번으로 옮겨주고 (2)탑을 3번으로 옮기면 다음과 같다.

이제 (2)탑 위에있던 (1)탑을 오른쪽으로 옮겨주면 (1,2)탑이 완성되어 아래와 같이 모든 탑을 3번으로 옮길 수 있게 된다.

결과적으로 총 3번의 움직임으로 탑을 1번에서 3번으로 옮길 수 있었다.

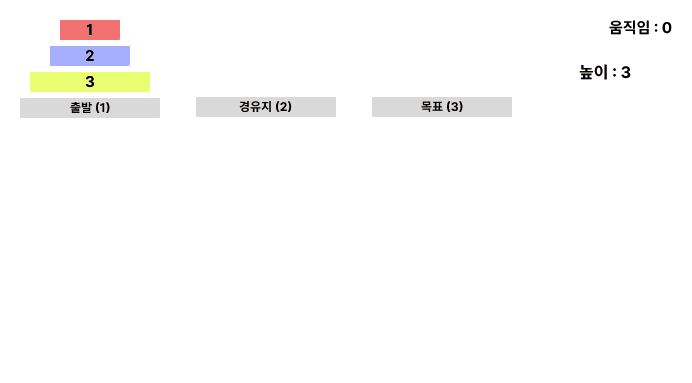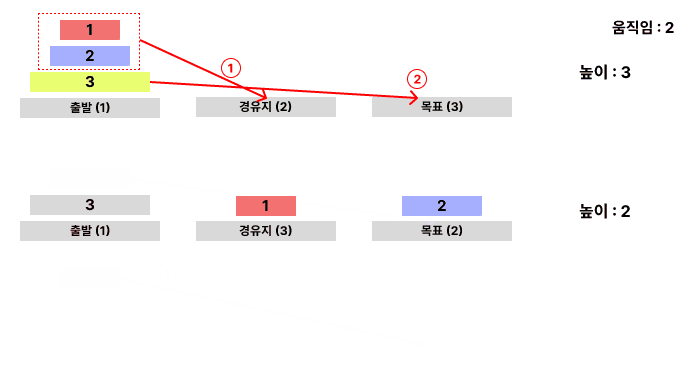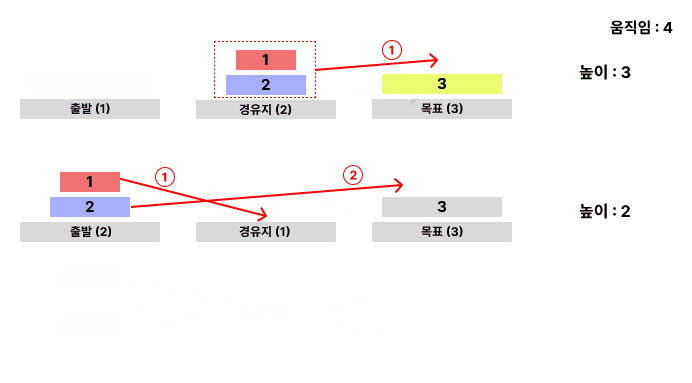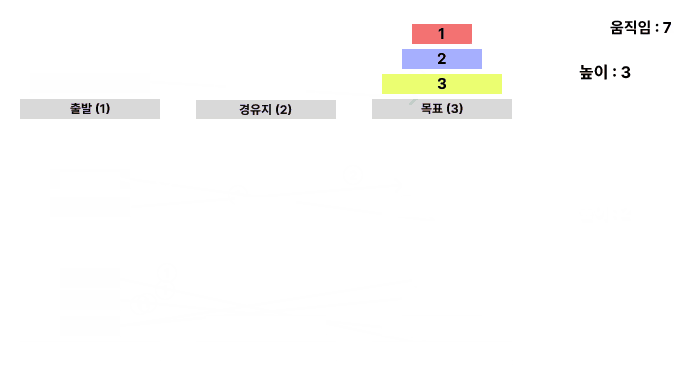
이제 높이가 3인 하노이의 탑을 옮겨보자.

우선 3번에 (1,2,3)탑이 있기 위해선 가장 밑에 있는 원판인 (3)탑이 3번으로 가야한다. 하지만 우리는 한번에 1개씩 밖에 원판을 움직이지 못하기 때문에 (1,2) 탑을 통째로 빈 공간인 2번으로 넘길 수 없다.

하지만 (1,2)탑을 통째로 옮기는 방법이 있어 2번으로 넘길 수 있다면 (3)탑을 3번으로 옮기고 (1,2)탑을 다시 3번으로 옮겨서 하노이 탑을 해결할 수 있다! 그러므로 옮겼다 셈 치고 로직을 만들면 다음과 같다.

1. 가장 밑의 원판인 (3)탑 위에있는 (1,2)탑을 빈칸인 2번으로 옮긴다.
2. (3)탑을 목표 위치인 3번으로 옮긴다.
3. 빈칸 위치인 2번 탑인 (1,2)를 다시 목표 위치였던 3번으로 옮긴다.

그러면 (1,2)탑을 어떻게 빈칸인 2번으로 옮길 수 있을까?? 보기 편하게 바닥의 이름을 변경하고 (1,2)탑만 보면 다음과 같다.

(1,2)탑의 요소인 (1)과 (2)만 움직일 것이므로 (3)탑은 마치 바닥과 같다. 왜냐하면 (3)탑 위의 요소는 모두 3보다 작기 때문에 (3)탑 위에 자유롭게 올라 갈 수 있기 때문이다! 이렇게 생각하면 아까 사용했던 로직을 그대로 적용할 수 있다.

1. 가장 밑의 원판인 (2)탑 위에있는 (1)탑을 빈칸인 3번으로 옮긴다.
2. (2)탑을 목표 위치인 2번으로 옮긴다.
3. 빈칸 위치인 3번 위에 있는 탑인 (1)을 다시 목표 위치였던 2번으로 옮긴다.

위의 로직을 적용한 경우를 애니메이션으로 보면 다음과 같다.

규칙이 보이는가?? 탑의 부분을 나누어서 생각해보니 똑같은 로직을 적용해 탑의 일부분을 나누어서 옮길 수 있고 최종적으로 모든 탑을 목표 위치인 3번으로 옮길 수 있다는 것을 알 수 있다. 즉 재귀를 이용하면 문제를 해결할 수 있다! 재귀를 적용한 코드를 보면 다음과 같다.

하노이탑움직이기(시작위치, 목표위치, 남은 위치, 옮기려는 탑의 높이){
        if(옮기려는 탑의 높이가 1이라면){
           //탑의 높이가 1이므로 옮길 수 있게된다.
           시작 위치에서 탑(원판)을 목표위치로 옮긴다.
        }else{
            //시작 위치에서 맨 밑의 원판위의 모든 탑을 남은 위치로 옮긴다.
            하노이탑움직이기(시작위치, 남은위치, 목표위치,옮기려는 탑의 높이-1)
            시작 위치에서 탑(맨 밑의 원판)을 목표위치로 옮긴다.
            //남은 위치의 탑을 모두 목표 위치로 옮긴다.
            하노이탑움직이기(남은위치, 목표위치, 시작위치,옮기려는 탑의 높이-1)
        }
    }

DP(재귀)를 적용한 시간복잡도를 다시 구해보자

위의 수도코드를 정리하면 다음과 같은 코드가 나온다.

public static void setHanoiRoute(int start, int end, int mid, int depth){
        if(depth == 1){
            route.add(new Move(start,end));
        }else{
            setHanoiRoute(start,mid,end,depth-1);
            route.add(new Move(start,end));
            setHanoiRoute(mid,end,start,depth-1);
        }
    }

함수가 한번에 2개씩 실행되고 최대로 실행될 개수는 최초의 탑의 높이이다. 그러므로 시간복잡도를 계산하면 다음과 같다.

O(n)
= (하노이탑 옮기기 + 하노이탑옮기기) ^ (최초 하노이탑의 높이)
= 2^N

아까 6^N보다 시간복잡도가 단축됐음을 알 수 있다. 경로를 출력해야할 최대 N의 크기는 20이므로 2^20 = 1,048,576은 제한시간인 6초인 6억보다 작다. 그러므로 위의 방식을 이용하면 N이 20까지의 경로는 모두 출력할 수 있다!

그러면 N=100인 경우는??

하지만 경로를 출력하지 않고 이동 횟수를 구해야 되는 N의 최대값은 100이다. 그러므로 기존 알고리즘을 사용하면 2^100 = 1,267,650,600,228,229,401,496,703,205,376이 나오기 때문에 제한 연산 횟수인 6억보다 커서 시간초과가 발생한다.

그러므로 굳이 경로를 출력하지 않아도 되는 경우(N>20)에는 일일히 탑을 옮기지 않고 이동 횟수를 찾을 수 있는 방법을 찾아야한다. 수의 규칙을 찾아보기 위해 N이 1~5까지의 경우의 수를 보면 다음과 같다.

N = 1, 1회
N = 2, 3회
N = 3, 7회
N = 4, 15회
N = 5, 31회

규칙이 보이는가?? 점화식으로 규칙을 표현해보면 다음과 같다.

A(n) = A(n-1)*2 + 1

N은 최대 100이기 때문에 위의 식을 반복문을 사용해 이동횟수를 구해도 제한시간내에 해결할 수 있다. 하지만 더 빠른 연산을 위해 식을 최적화하면 다음과 같다.

A(n) = A(n-1)*2 + 1
A(n)+1 = 2*(A(n-1) + 1)
A(n) +1 = 2^N
A(n) = 2^N - 1

위의 식을 이용하면 반복문을 사용하지 않고 점화식을 이용해 O(1)의 시간복잡도로 이동횟수를 구할 수 있다! 이때 N은 최대 100이기 때문에 최대값은 1,267,650,600,228,229,401,496,703,205,375이다. long범위로도 커버가 되지 않는 범위이기 때문에 큰 수 연산을 할때 사용하는 BigInteger를 이용해 이동횟수를 구하면 문제를 해결할 수 있다.

코드

import java.math.BigInteger;
import java.util.*;
import java.io.*;

public class Main {
    static List<Move> route = new ArrayList<>();

    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader((System.in)));

        int N = Integer.parseInt(br.readLine());
	
    	//2^N-1 연산
        BigInteger count = (new BigInteger("2")).pow(N).subtract(new BigInteger("1"));

        System.out.println(count.toString());

        if(N <=20){
            setHanoiRoute(1,3,2,N);
            for(Move m : route){
                System.out.println(m.start+" "+m.end);
            }
        }
    }

    public static void setHanoiRoute(int start, int end, int mid, int depth){
        if(depth == 1){
            route.add(new Move(start,end));
        }else{
            setHanoiRoute(start,mid,end,depth-1);
            route.add(new Move(start,end));
            setHanoiRoute(mid,end,start,depth-1);
        }
    }
}
//이동 경로 클래스
class Move{
    int start;
    int end;

    public Move(int start, int end){
        this.start = start;
        this.end = end;
    }
}

실행 결과

제한시간인 6초안에 문제가 해결 되었다!

키워드

최소 이동 횟수
- 최소~라는 말이 붙으면 완전탐색, DP의 가능성을 가지고 있다

팁

한번에 움직이지 못한다는 것은 로직상 한번에 여러개를 움직일 수 있게 만들 수 있기 때문에 DP의 가능성을 생각해보자.
어떻게 전체다 옮기지??라고 생각할 때 일부분만 한번 옮겨보자. DP적인 생각을 하는데 큰 도움이 된다.
점화식을 만들어 보기 위해 경우의 수는 5번까지 해본다. 가끔 n-3까지 쓰는 경우가 있다.

'알고리즘 문제 풀이 > 해설' 카테고리의 다른 글

[백준 14226][Gold 4] - 이모티콘 (JAVA) (2)	2024.02.07
[백준 1700][Gold 1] - 멀티탭 스케줄링(JAVA) (0)	2024.02.05
[백준 15988][Silver 2] - 1, 2, 3 더하기 3(JAVA) (0)	2024.02.03
[백준 1744][Gold 4] - 수 묶기(JAVA) (0)	2024.02.02
[백준 5427][Gold 4] - 불(JAVA) (1)	2024.01.31