[백준 - 1092][Gold 5] - 배 (JAVA)

문제
지민이는 항구에서 일한다. 그리고 화물을 배에 실어야 한다. 모든 화물은 박스에 안에 넣어져 있다. 항구에는 크레인이 N대 있고, 1분에 박스를 하나씩 배에 실을 수 있다. 모든 크레인은 동시에 움직인다.
각 크레인은 무게 제한이 있다. 이 무게 제한보다 무거운 박스는 크레인으로 움직일 수 없다. 모든 박스를 배로 옮기는데 드는 시간의 최솟값을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 N이 주어진다. N은 50보다 작거나 같은 자연수이다. 둘째 줄에는 각 크레인의 무게 제한이 주어진다. 이 값은 1,000,000보다 작거나 같다. 셋째 줄에는 박스의 수 M이 주어진다. M은 10,000보다 작거나 같은 자연수이다. 넷째 줄에는 각 박스의 무게가 주어진다. 이 값도 1,000,000보다 작거나 같은 자연수이다.
출력
첫째 줄에 모든 박스를 배로 옮기는데 드는 시간의 최솟값을 출력한다. 만약 모든 박스를 배로 옮길 수 없으면 -1을 출력한다.
단순 구현으로 풀릴까?
우선 가장 쉬운 방법인 구현을 생각해보자.
각 박스를 운송이 가능한 크레인이 있는 배에게 실는 가능한 모든 조합의 수는 (박스의 개수)^(크레인의 수) 이다.
(박스의 개수) = 10,000 이고 (배의 개수) = 50 이기 때문에 최대 연산 횟수는 10,000^50 이다. 이는 시간제한인 2초의 최대 연산 횟수인 2억보다 훨신 큰 수이므로 조합을 이용한 구현으로는 이 문제를 제한된 시간 내에 해결할 수 없다.
DP로 풀릴까??
DP로 풀기 위해선 점화식을 만들어야한다. 현재 우리가 구해야 하는 값은 최소 걸린시간이므로 시간을 값이라고 두었을 때 dp배열을 만들기 위해 상태를 생각해보면 다음과 같은 DP 배열을 만들 수 있다.
dp[크레인의 종류][현재까지 옮긴 박스의 조합] = 걸린 시간
하지만 박스의 조합은 말했든 10,000^50이기 때문에 배열의 크기로 두기에 너무 커 부적절하기 때문에 DP로는 풀 수 없을 것 같다. 우린 다른 방법을 생각해야 한다.
그리디로 풀릴까??
그리디로 풀기 위해선 현재 가장 이득이 되는 행동과 현재 가장 손해를 보는 행동을 찾아야한다. 가장 손해를 보는 행동은 무거운 무게를 들 수 있는 크레인이 무게가 작은 크레인을 드는 경우이다.
만약 화물이 1,1,1,9,9 이고 크레인이 2,3,9인 경우 크레인이 무게가 가장 작은 화물을 드는 경우를 시뮬레이션해보면 다음과 같다.
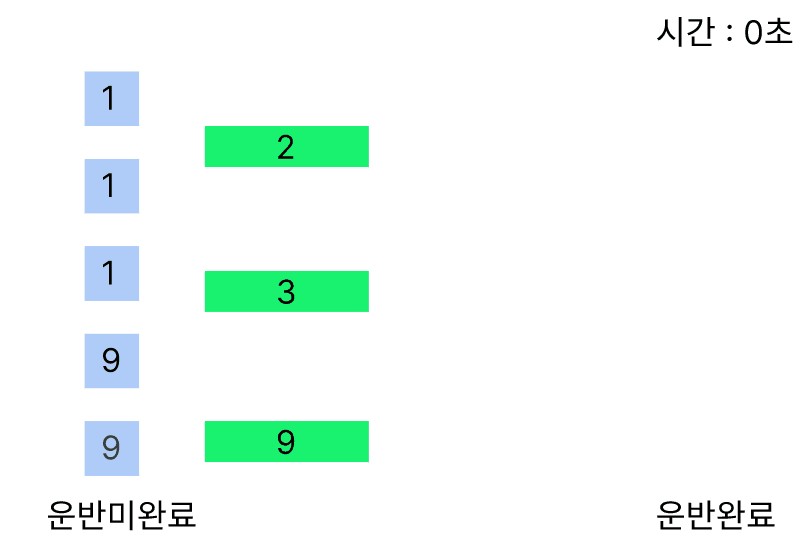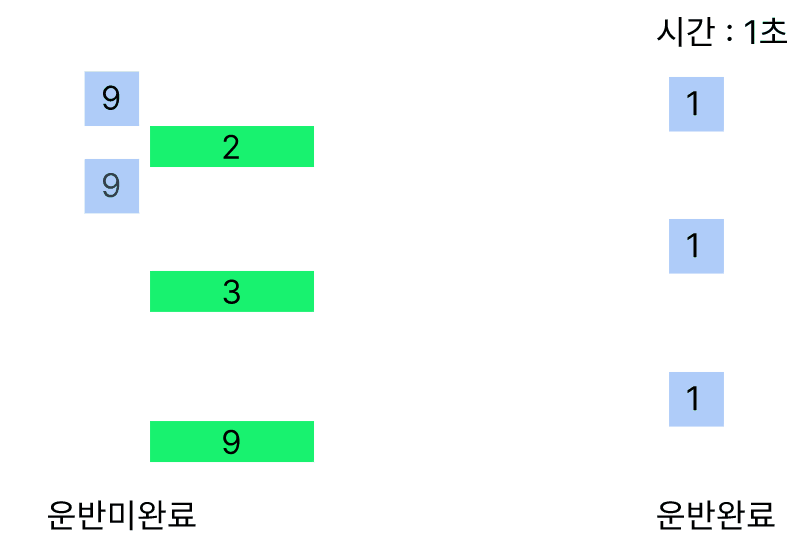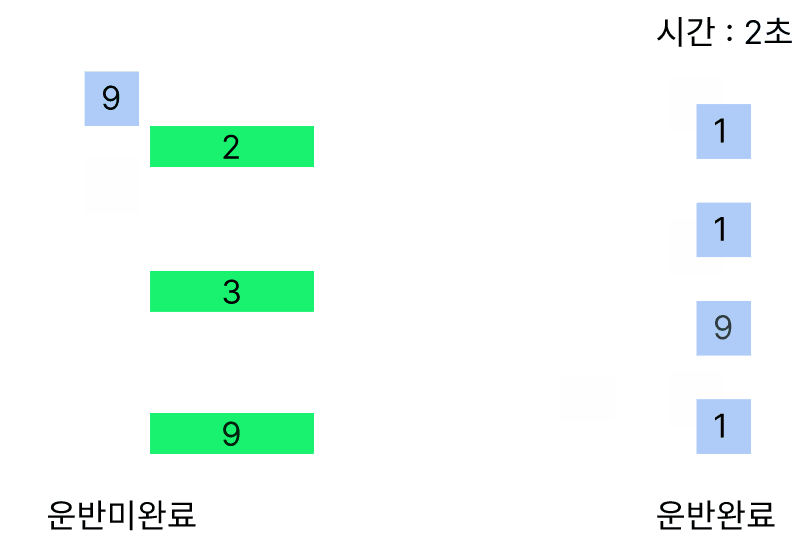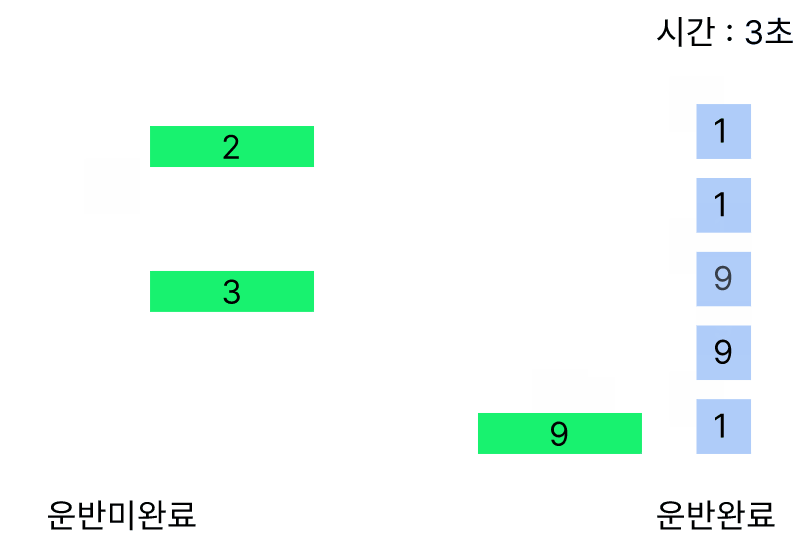
0초의 경우에 모든 크레인이 모든 화물을 1개씩 들지만 1초부터 9번 크레인만이 무게가 9인 화물을 옮길 수 있어 혼자 2번 옮기게 되어 3초가 걸린다.
반대로 가장 이득을 보는 행동은 무거운 무게를 들 수 있는 크레인이 무게가 가장 무거운 크레인을 드는 경우이다. 이 경우를 시뮬레이션하면 다음과 같다.
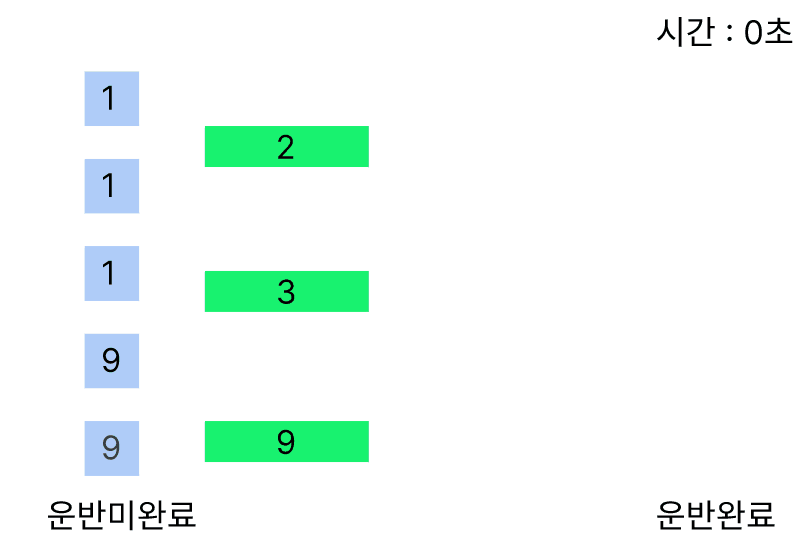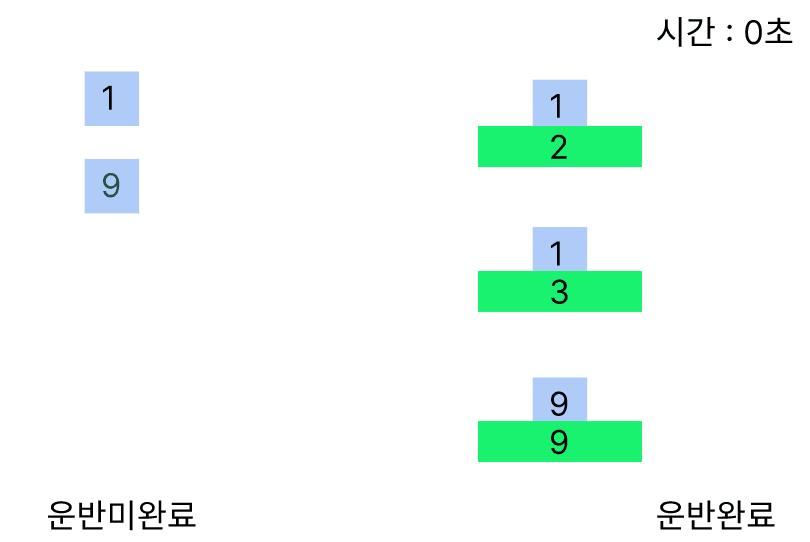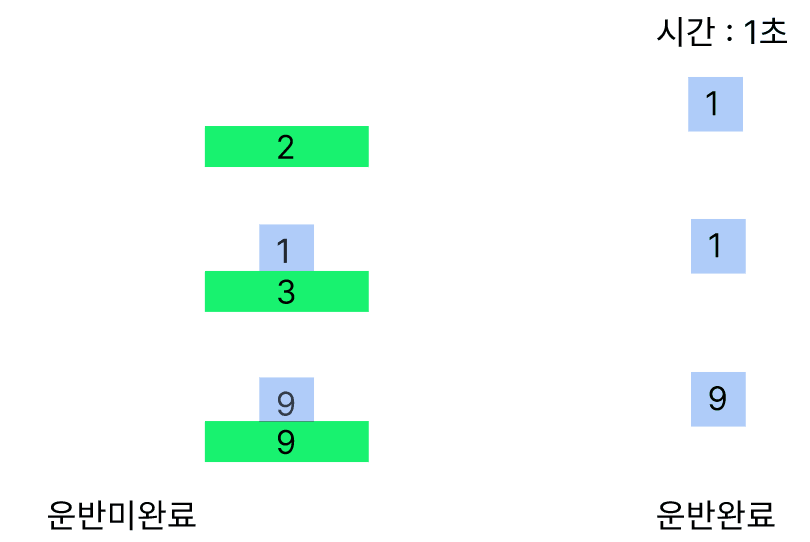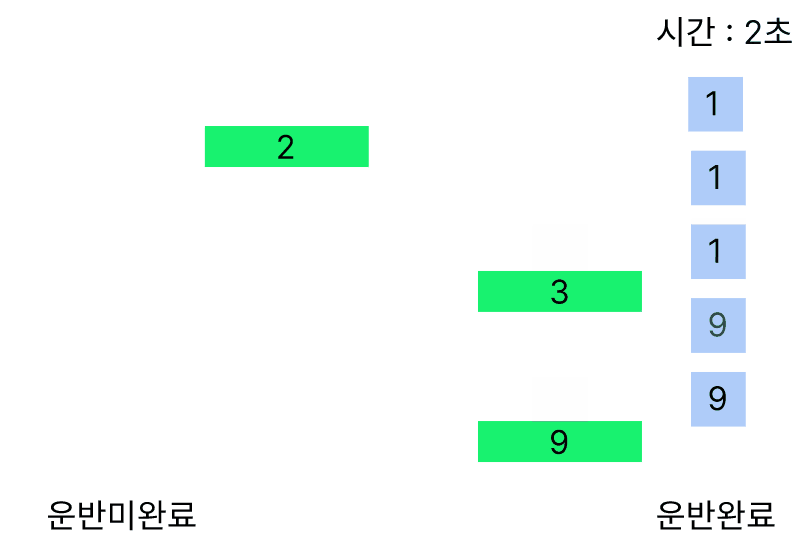
이번엔 9번 크레인이 화물이 9인 무게를 들다 1초인 시점에 1화물과 9화물이 남아 3번 크레인이 1무게의 화물을 들 수 가 있게되어 2초안에 모든 화물을 옮길 수 있게 되었다.
그러므로 가장 무거운 크레인이 가장 무거운 화물을 옮기게 한다면 가장 효율적인 움직임으로 화물을 옮길 수 있기 때문에 최단 시간으로 모든 화물을 옮길 수 있다!
그리디 알고리즘의 시간복잡도를 구해보자
위의 알고리즘을 반영한 시간 복잡도는 다음과 같다.
O(n)
= (무거운 화물을 찾기위한 화물 정렬) + (화물의 개수)/(크레인의 개수)
= MlogM+ M/N
≒ MlogM
최악의 경우는 한개의 배가 모든 화물을 옮기는 경우이다. 이때 최대 연산 횟수는 10,000*log(10,000) + 10,000이므로 이는 제한시간인 2초의 연산 횟수인 2억보다 작다. 그러므로 그리디를 이용하면 문제를 해결할 수 있다!
코드
import java.util.*;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
public class Main {
final static int INF = -1;
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader((System.in)));
int N = Integer.parseInt(br.readLine());
int[] craine = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
Arrays.sort(craine);
int M = Integer.parseInt(br.readLine());
List<Integer> readyExpressList = new ArrayList<>(List.of(Arrays.stream(br.readLine().split(" ")).map(Integer::valueOf).toArray(Integer[]::new)));
//무거운 화물을 찾기위한 내림차순 정렬
Collections.sort(readyExpressList,Collections.reverseOrder());
int time = 0;
//화물 운송
while(!readyExpressList.isEmpty()){
boolean move = false;
//가장 무거운 화물을 옮길 수 있는 크레인이 가장 무거운 화물을 옮기도록 탐색
for(int i = N-1; i>=0;i--){
for(int j=0;j<readyExpressList.size();j++){
if(readyExpressList.get(j) <= craine[i]){
readyExpressList.remove(j);
move = true;
break;
}
}
}
//못옮겼다면 -1출력
if(!move){
time =INF;
break;
}
time++;
}
System.out.println(time);
}
}
실행 결과

키워드
- 최단시간
- 완전탐색, DP, 그리디의 가능성을 가지고 있다.